Understanding the Ilmango Tunnel Bore

Specifically, this is about his Industrial Mining Machine, Designing a Honey Tunnel Bore and the Large Honey Tunnel Bore from his Peaceful Challenge. Ilmango provides a world download for the machines shown in the first video.

At the core of both designs are 2 lines of single-step insta-wire. One controls the dupers, which are spaced out on every fifth block. The other insta-wire controls TNT catapults that launch the duped TNT in the air in front of the machine.

The delay between the dupers and the launchers is crucial. It is provided by a flying machine that is returned by a single stepping return station.

Flying Machine Timings

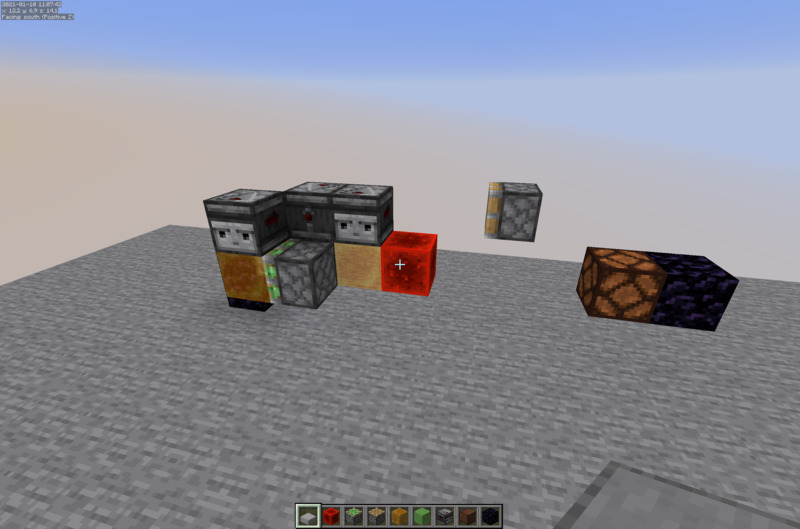
The images show the flying machine I used to simulate the one in the tunnel bores. It is a standard 2 way Flying Machine in a Honeblock configuration. The payload is the Redstone block that will activate the lamp, and it has an additional observer that will activate the return station.

In general, such a 2 way flying machine takes 10 game ticks per step, but this breaks down into 4 gt for the push and 6 game ticks for the pull.

\[t_{travel} = (6 + 4)d = 10d\] \[t_{act} = 9d + 4\] \[t_{deact} = 9d + 2\]

So here, the flying machine will fully arrive at the return station after 30 game ticks, but the redstone block is already in place for the last 6 game ticks - the lamp will turn on after 24 game ticks.

The observer activated by the return station will fire one game tick earlier than the one that would continue the current direction of travel. So the last step is cut short by one game tick.

Now, on the way back the flying machine will travel one block further and remove the powersource of the instant-wire piston. This is \(t_{deact}\) above, and it occurs after 2 game ticks into the step. The observer observes, and as the piston begins to push the redstone block turns into Block 36 which instantly cuts the power.

So the total time to travel 3 blocks in one direction and deactivating the powersource 4 blocks in the other direction is 61 game ticks.

\[t_{insta} = 3*10 + 3*10 - 1 + 2 = 61\]

Space consideration

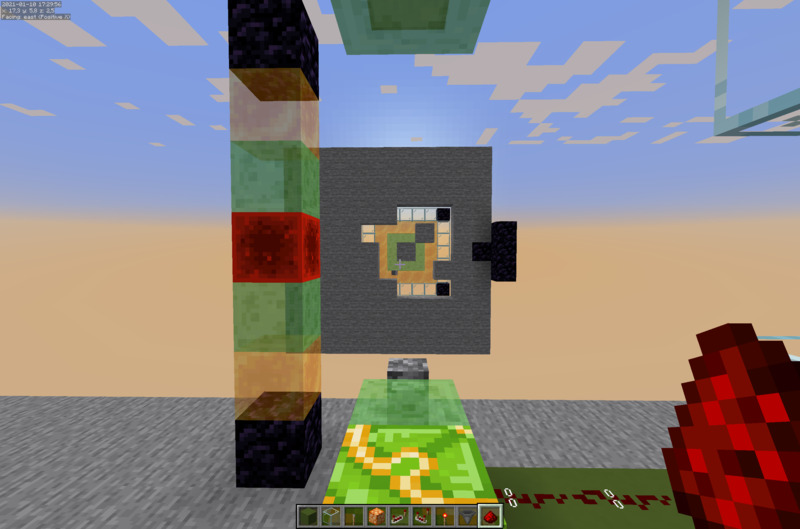
A catapult based tunnel bore will generally make a hole like this: 7x7 in size, with a 5x5 are in the center where sticky blocks can be used.

Size matters: Hole Dimensions per Duper/Catapult

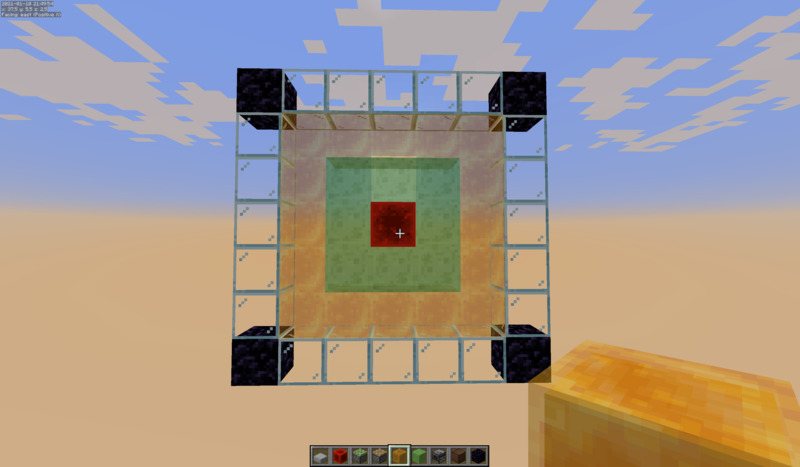
The obsidian shows the problematic positions: the y-coordinate and the front/back position of the exploding TNT is always the same. But there is some randomness to the left/right position, and these blocks do not always get blown up.

If you have multiple catapults/dupers, the tunnel will always be at least 7 m high as long as you put a catapult on every 5th block (i.e. catapult, 4 blocks of space, catapult). If you space them out further than that, blocks will be left over in these positions, especially if you are blasting through blocks with high blast resistance.

For a single duper/catapult, these corner blocks will also sometimes stay behind. It is a sign that we are meant to leave out the corners in out portals.

As I want to be able to space my catapults out if I am not interested in a regular tunnel shape, I will keep any sticky blocks in these 5x5 regions, and when linking up multiple segments I will keep them in the central 3 blocks (the slimeblock region in the image).

The All-Important Y-Position

The timings are critical because they determine the Y-position of the explosion.

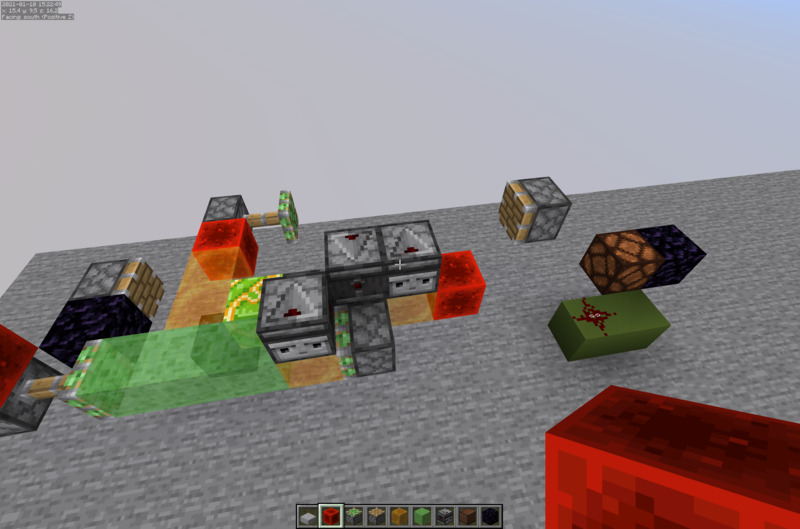
The contraption in the image has the same timings and height as the catapult used in the Ilmango Tunnel Bores. The upper piston needs 2 gt delay because here it moves the block on the push. Also the upper slimeblock needs to be 1m back because the lower part is not moving.

I want to find the delay that gives the most central explosion. And I want to obtain the fuse time of the TNT in the moment the vertical piston fires (this is when the redstone lights up/when the observers in the catapult flash red).

Delay	TNT fuse on catapult activation / explosion position
60 gt	fuse 19, explosion low by 2
61 gt	fuse 18, explosion low by 1
62 gt	fuse 17, explosion low by 0.75
63 gt	fuse 16, explosion low by 0.5
64 gt	fuse 15, explosion a little bit low
65 gt	fuse 14, explosion a little bit high
66 gt	fuse 13, explosion high by 0.5
67 gt	fuse 12, explosion high by 0.75
68 gt	fuse 11, explosion high by 1
69 gt	fuse 10, explosing high by 1

For the most promising candidates I also fired the catapult at a wall and counted how many blocks were destroyed above and below the intended vertical center of the explosion.

Delay	Distance	High	Low
64 gt	14 m	10	15
64 gt	14 m	9	16
64 gt	14 m	10	15
65 gt	13 m	13	15
65 gt	13 m	14	13
65 gt	13 m	14	15
66 gt	13 m	8	5
66 gt	13 m	13	6
66 gt	13 m	7	4

65 game ticks of delay seems to be pretty centered, I guess it did not seem that way because the eye has a tendency to follow the movement. This seems like an ideal value for a centered design.

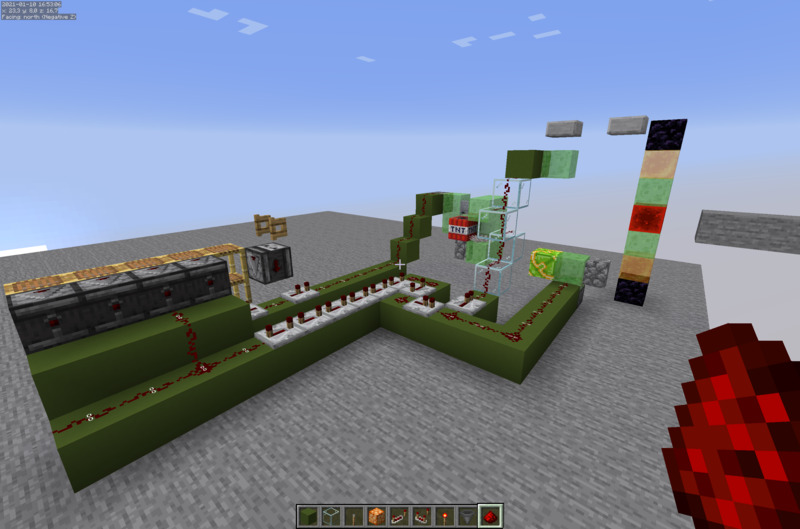
Timings for the Whole Machine

• gt 1: duper single steppers begin retracting
• gt 3: flying machine observer fires
• gt 9: duper dupes (single stepper + extension delay), tnt fuse=79. from here on, \(gt = 9 + (79 - fuse) = 88 - fuse\)
• gt 27: flying machine activates return station
• gt 31: flying machine finished retraction, observer starting in other direction fires
• gt 62: flying machines removes redstone block for catapult stepper
• gt 66: fuse=22, single stepper observer fires
• gt 70: fuse=18, catatapult extension observer fires
• gt 74: MAGIC FUSE = 14, catapult observers fire

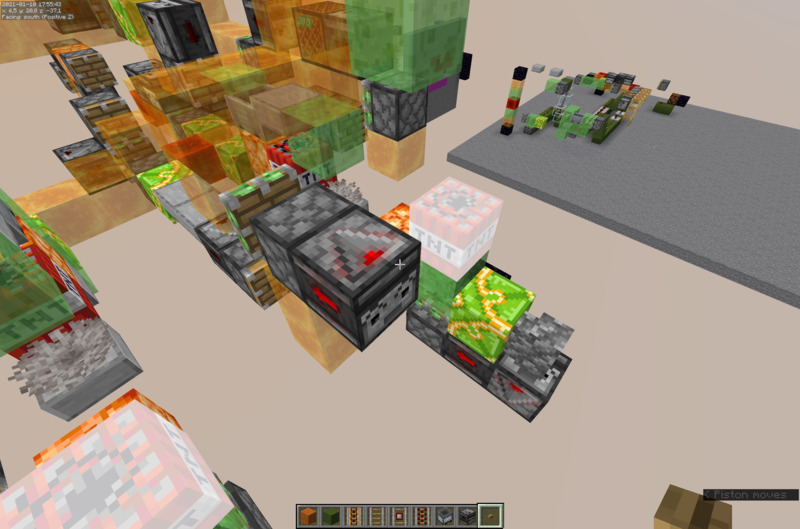
The pistons in the catapult are activated when the observers flash red. This is the easiest method of verifying the timings for the machine: tick freeze, activate machine, tick step until the observers flash and verify that the TNT has a fuse time of 14.

61 game ticks of delay come from the flying machine, where do the additional 4 come from?

The instant wire for duper and catapult is identical, but the duper is activated the instant the duper extension starts pushing. But the catapult observers add an additional 2 game ticks after the extension has completed the push, which also takes 2 game ticks.